Ohm és Kirchoff törvényei

A fejezet tartalma:
Az alábbiakban az egyenáramú áramkörök legfontosabb összefüggéseiről lesz szó. Ezek segítségével méretezhetjük áramköreinket (hogy az történjen bennük, amit mi szeretnénk...), illetve egy adott kapcsolás esetén ki tudjuk számolni, hogy hol mekkore feszültségek illetve áramok mérhetők, ha a kapcsolást megépítjük.

Ohm törvénye

Kapcsoljunk össze egy aktív és egy passzív elemet, például egy feszültséggenerátort és egy ellenállást! Ez a legegyszerűbb áramkör. A feszültséggenerátor feszültsége az ellenállás és a vezeték szabad töltéshordozóit mozgásba hozza - az áramkörben áram folyik. A feszültséggenerátor lesz az energia forrása (vagy áramforrás), az ellenállás pedig a fogyasztó, amely "elfogyasztja" az elektromos energiát.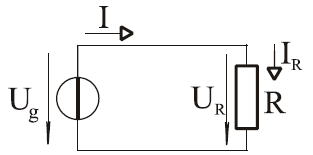
 

1. ábra: A legegyszerűbb áramkör

Ha változtatjuk a feszültséget (pl. labortápegységet használunk, vagy több elemet kapcsolunk össze), akkor azt tapasztaljuk, hogy az ellenálláson eső feszültség értéke a rajta átfolyó árammal egyenesen arányos, az arányossági tényező az itt fogyasztóként használt ellenállás értéke.Ez Ohm törvénye.



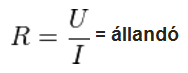
Kísérletezzünk szimulációs program segítségével!

A fenti kapcsolás legegyszerűbb kipróbálásához használjunk szimulációs programot! A szimuláció előnye, hogy nem kerül pénzbe (ha már van számítógépünk...), nem gyújtjuk fel vele a lakást. Az University Colorado honlapján PHET interaktív szimulációk néven érdekes programok találhatók, melyek közül most az "Áramkörépító csak egyenfeszültségre" nevű programot használjuk. Az áramköri lemeket az egérrel húzhatjuk a rajzterületre, s a vezeték (barna sáv) elem többszöri használatával köthetük össze a kapcsolást. A fenti példához egy elemet használunk áramforrásként, s ellenállás helyett most egy izzólámpát választottunk. Mindkét alkatrész paraméterei változtathatók. Az összefüggések megfigyeléséhez szükségünk lesz a feszültségmérő és az árammérő modulokra is.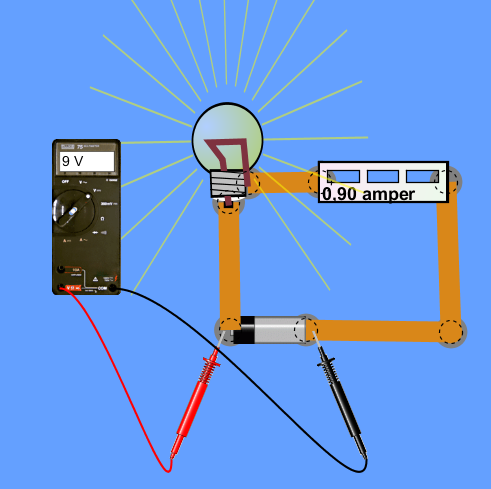


2. ábra: Kísérleti áramkör szimulációja a PHET Áramkörépítő programmal

Változtassuk az áramkört tápláló áramforrás feszültségét, és jegyezzük fel a hozzá tartozó áram értékét! Amint látjuk, esetünkben az U/I hánydos mindig 10 V/A. Ez azt jelenti, hogy az izzó ellenállása 10 Ω.
U [V]
 3
 6
 9
 12
 15
I [A]
 0,3
 0,6
 0,9
 1,2
 1,5
A fenti szimuláció meglehetősen idealizált. Egy valóságos kísérletben ettől eltérő összefüggést tapasztalnánk. Az eltérés okai (amit a fenti szimuláció nagyvonalúan elhanyagol):

Kirchhoff I. törvénye: a csomóponti törvény

A villamos hálózat olyan áramkör, amely több fogyasztót, vagy több generátort tartalmaz. Az összetett áramkör fontos részei a csomópont, az ág és a hurok. A csomópont áramai közötti kapcsolatot Kirchhoff csomóponti törvénye mutatja meg.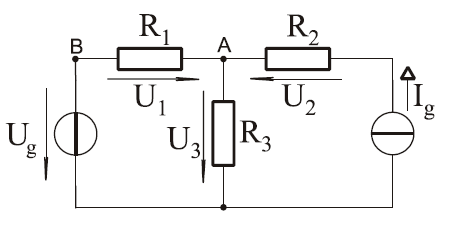


3. ábra: Csomópontokkal rendelkező összetett áramkör

Három vagy több vezeték találkozási pontja a hálózat csomópontja. A 3. ábrán például az R3 ellenállás két végénél találunk egy-egy csomópontot. Egy csomópontba ágak futnak be. Az ágakhoz befolyó vagy kifolyó áramok rendelhetők. Kirchhoff csomóponti törvénye szerint a csomópontba befolyó áramok összege megyegyezik a csomópontból kifolyó áramok összegével, azaz a csomópont áramainak előjelhelyes összege nulla. Az összegzéskor a befolyó és a kifolyó áramokat ellentétes előjellel kell figyelembe venni.



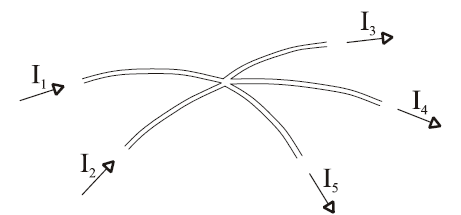
4. ábra: Egy csomópontba befolyó és kifolyó áramok




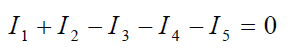
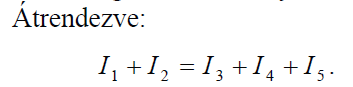
Nézzünk egy példát!

Mekkora és milyen irányú áram folyik az R3 ellenálláson keresztül, ha az A csomópontba R1 és R2 felől is 1 A áram folyik be?

Megoldás: Ha I1 és I2 befolyó áramok, akkor Kirchoff csomóponti törvénye szerint I3 az A csomópontból szükségszerűen kifolyó áram lesz, nagysága pedig  I3 = I1 + I2 = 1 A + 1 A = 2 A.

Kirchoff II. törvénye: a huroktörvény

A hurok a villamos hálózatban egy tetszőleges zárt körüljárás. Az egyszerűség kedvéért a hurok képzésekor a hurokba bevonni kívánt hálózatelemeket csak egyszer járjuk át, de ez nem kötelező. Egy ilyen, általános hálózatból kiemelt hurok látható az 5. ábrán.


5. ábra: Egy összetett áramkörből kiemelt hurok

Kirchoff II. törvénye szerint a hurokban szereplő feszültségek előjelhelyes összege nulla. Válasszunk a példaként szereplő hurokban egy kiinduló csomópontot, A-t és egy körüljárási irányt, például az óramutató járásának megfelelően! Az A csomópontból kiindulva, és a választott körüljárással egyező irányú feszültségeket pozitívnak véve írható:



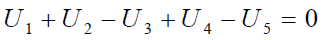
A Kirchoff huroktörvény általános alakja:


A fentebb ismertetett három törvény: az Ohm törvény, valamint Kirchhoff I. és II. törvénye a villamos hálózatokkal kapcsolatos számítások három alaptörvénye. Az egyenáramú hálózatoknál gyakran előforduló soros és párhuzamos kapcsolásra is ezen három alaptörvény segítségével fogunk törvényszerűségeket megállapítani.

Soros kapcsolás

Azt mondjuk, hogy két kétpólus sorba van kapcsolva, ha egy-egy kivezetésükkel össze vannak kötve és erre
az összeköttetésre nem csatlakozik harmadik ág. Kétpólusnak a villamos hálózatok két kivezetéssel rendelkező elemeit nevezzük. Az előző fejezetben tárgyalt aktív és passzív áramköri elemek mindegyike kétpólus, mert két kivezetésük van.


6. ábra: Áramköri elemek soros kapcsolása

A soros kapcsolás egyik fő jellemzője az, hogy a sorba kapcsolt elemeken azonos áram folyik keresztül. A fenti ábra jelöléseivel: IG = IR. A fenti ábrán látható kapcsolásban könnyen belátható, hogy az áramgenerátorból kiáramló töltések csak az ellenálláson tudnak továbbhaladni, ezért időegységenként az ellenálláson ugyanannyi töltéshordozó halad át, mint amennyi az áramgenerátoron.

A soros kapcsolás másik jellemzője az, hogy a sorosan kapcsolt elemeken az eredő feszültséget az elemeken eső részfeszültségek (előjelhelyes) összegeként számíthatjuk. Ennek belátásához kapcsoljunk sorba két feszültséggenerátort az alábbi ábra szerint.


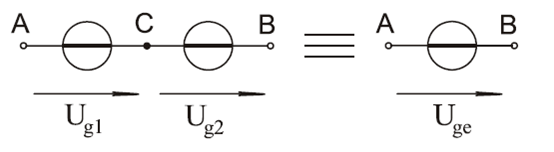
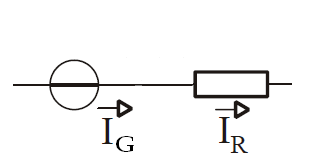
7. ábra: Feszültséggenerátorok sorba kapcsolása

A két generátor eredő feszültsége a huroktörvény alapján: UAB = Ug1 + Ug2.

A két feszültséggenerátort helyettesíthetjük egyetlen eredő feszültséggenerátorral amelynek forrásfeszültsége a két generátorfeszültség összege. Uge = Ug1 + Ug2.

Megjegyzés: A helyettesítés után a C pont az áramkörből eltűnik, többé már nem hozzáférhető!

Párhuzamos kapcsolás

Azt mondjuk, hogy két kétpólus párhuzamosan van kapcsolva, ha mindkét kivezetésükkel össze vannak kötve.Ha több kétpólus van mindkét kivezetésével összekötve, akkor azt mondjuk, hogy mindegyik párhuzamos kapcsolásban van egymással.


8. ábra: Kétpólusok párhuzamos kapcsolása

Párhuzamosan kapcsolt elemeken a feszültség azonos: U1 = U2. Ez belátható, ha a két párhuzamosan kapcsolt elem által alkotott hurokra alkalmazzuk Kirchoff huroktörvényét.

Párhuzamosan kapcsolt elemeken az eredő áramot az egyes ágak vagy áramának előjelhelyes összegeként számíthatjuk: I = I1 + I2. Ez könnyen belátható, ha pl. a B csomópontra pontra alkalmazzuk Kirchoff csomóponti törvényét.

Sorba kapcsolt ellenállások eredője

Ha néhány ellenállást sorbakötünk, akkor a soros kapcsolás tulajdonságai alapján azt mondhatjuk, hogy:

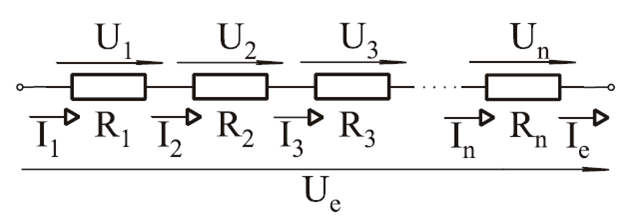
9. ábra: Ellenállások soros kapcsolása

Létezik egy fiktív, eredő ellenállás, amely az eredő feszültség és az eredő áram hányadosaként számítható. Erre is érvényes, hogy kétszer, háromszor, négyszer nagyobb feszültség hatására kétszer, háromszor, négyszer nagyobb áram folyik. Próbáljuk meg az Res = Ue/Ie értékét a részellenállások értékével kifejezni!




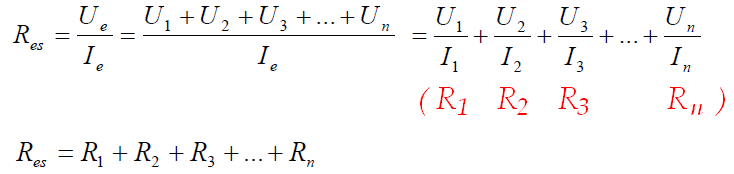
A fentiekből az is következik, hogy a sorosan kapcsolt ellenállások eredője minden részellenállásnál nagyobb. Bármilyen kis ellenállást kapcsolunk sorosan egy tetszőlegesen nagy ellenállással, az eredő nagyobb lesz a nagy ellenállásnál is, mert a töltéshordozóknak nagyobb akadályt kell leküzdeniük, hogy keresztülhaladjanak.

A sorba kapcsolt ellenállások egy speciális esete az, amikor n darab azonos értékű ellenállást kapcsolunk sorosan. Ekkor az eredő ellenállás a soros elemek ellenállásának n-szerese lesz.

Párhuzamosan kapcsolt ellenállások eredője

Párhuzamosan kapcsolt ellenállások is helyettesíthetők egyetlen eredő ellenállással.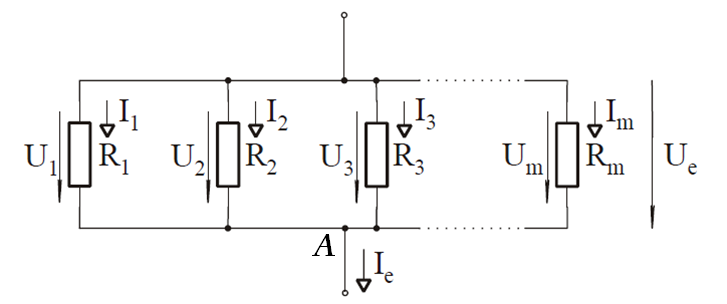


10. ábra: Ellenállások párhuzamos kapcsolása

Alkalmazzuk Kirchoff csomóponti törvényét az A csomópontra!


Kirchoff huroktörvénye szerint a párhuzamosan kapcsolt kétpólusokon eső feszültség azonos:


Ohm törvénye alapján:


Párhozamos kapcsolás esetén is felírhatjuk az eredő ellenállást az eredő feszültség és az eredő áram hányadosaként:


Az egyenlőség mindkét oldalát eloszthatjuk az Ue eredő feszültséggel, s ekkor ezt kapjuk:



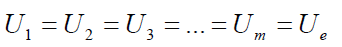
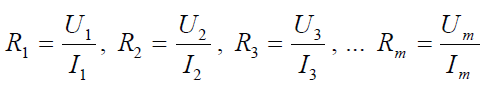
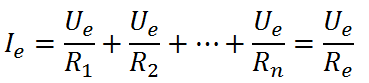
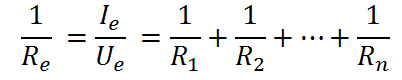
Két párhuzamosan kapcsolt ellenállás eredője

Legegyszerűbb esetként nézzük meg két párhuzamosan kapcsolt ellenállás eredőjét!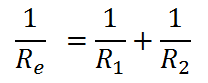



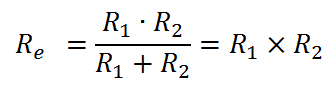
A jobbildali kifejezést közös nevezőre hozva, majd a kifejezés reciprokát véve ezt kapjuk:

Az X jelölés neve "replusz", amelyet csupán a tömörebb felírás kedvéért vezetünk be. Elsősorban összetett kifejezések közötti párhuzamos eredő számításának jelölése esetén előnyös használata.

Feszültségosztó

Két ellenállás sorba kapcsolásával feszültségosztót alakíthatunk ki. A tápláló feszültség megoszlik az R1 és R2 ellenállások között, innen származik a feszültségosztó elnevezés. Egyenáramú hálózatban a rendelkezésre álló feszültségnél nagyobb feszültség nem állítható elő. Feszültségosztóban a feszültség az ellenállásokkal egyenes arányban oszlik meg.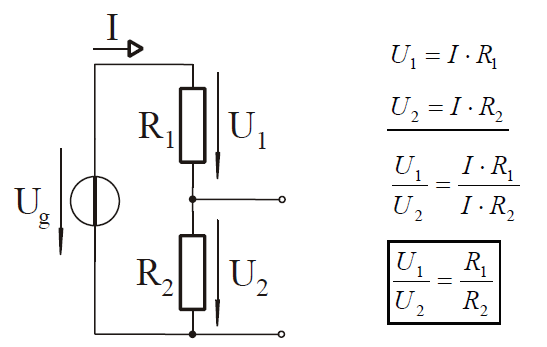

11. ábra: Feszültségoszó kapcsolás

Határozzuk meg most a feszültségosztó kimenő feszültségének, U2-nek az értékét a tápláló feszültség Ug és az ellenállások ismeretében!

Az R2 ellenálláson eső feszültség: 
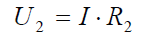
Ebből az I áram felírható a forrásfeszültség és az eredő ellenállás hányadosával:
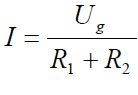
Behelyettesítés után ezt kapjuk:

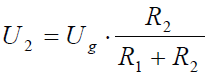
Felhasznált anyagok: